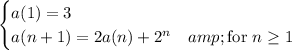Question

Find a recurrence relation for the number of n-digit ternary sequences in which no 1 appears anywehere to the right of a 2

Answer 1

Let
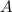
`A` denote the set of such sequence of length
`n`, and take
`a(n)` to be the size of
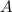
`A`, i.e. the number of such sequences of length
`n` consisting of digits 0, 1, or 2.

Split up this set of sequences according to whether a given sequence contains a 2 or does not contain a 2. Let's denote these subsets by
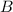
`B` and
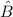
`\hat B`, respectively, and denote their sizes by
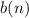
`b(n)` and
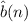
`\hat b(n)`. Clearly,
`a(n)=b(n)+\hat b(n)`.

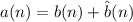
Since every sequence in
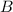
`B` contains a 2, the only new digit we can append to these sequences must be a 0 or a 2. On the other hand, to every sequence in
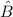
`\hat B` we can add any of 0, 1, or 2. So,


`a(n+1)=2b(n)+3\hat b(n)`

`\implies a(n+1)=2a(n)+\hat b(n)`


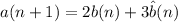
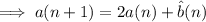
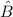
`\hat B` is the set of all sequences not consisting of 2s, which means
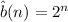
`\hat b(n)=2^n`. There are 3 possible such sequences of length 1, so we can recursively define the total number of such sequences by


`\begin{cases}a(1)=3\\a(n+1)=2a(n)+2^n&\text{for }n\ge1\end{cases}`