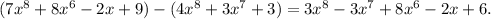Question

Which polynomial represents the difference below? 7x8 + 8x6 - 2x + 9 - (4x8 + 3x7 + 3)

Answer 1

Consider the difference of polynomials
`(7x^8 + 8x^6 - 2x + 9) - (4x^8 + 3x^7 + 3).`

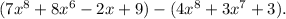
The first thing you have to do is take that "minus" sign through the parentheses containing the second polynomial (just change sign + to - and sign - to +):

`(7x^8 + 8x^6 - 2x + 9) - (4x^8 + 3x^7 + 3)=7x^8+8x^6-2x+9-4x^8-3x^7-3.`

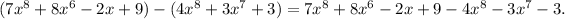
Then combine terms with the same degree:

`7x^8+8x^6-2x+9-4x^8-3x^7-3=(7x^8-4x^8)-3x^7+8x^6-2x+(9-3).`

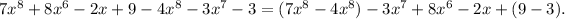
Note that

`7x^8-4x^8=(7-4)x^8=3x^8,\\ \\9-3=6.`

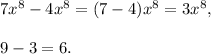
Thus,

`(7x^8 + 8x^6 - 2x + 9) - (4x^8 + 3x^7 + 3)=3x^8-3x^7+8x^6-2x+6.`

Answer 2

Use associativity and distributivity properties:

`7x^8 + 8x^6 - 2x + 9 - (4x^8 + 3x^7 + 3)=(7-4)x^8-3x^7+8x^6-2x\\+(9-3)\\=3x^8-3x^7+8x^6-2x+6`
We are done.