Answer:
Option a.
Explanation:
Two rectangles are similar. Height of one rectangle is 3 inches and height of second rectangle is 9 inches.
Let width of rectangles are x inches and y inches.
Then width of the second rectangle will be in the same ratio as of their heights.
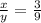
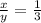 ⇒ x =
⇒ x =

Now perimeter of first rectangle P₁ = 3 + 3 + x + x = 2x + 6
Perimeter of second rectangle P₂ = 9 + 9 + y + y = 18 + 2y
Ratio of P₁ and P₂ =

=
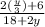 [as
[as
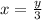 ]
]
=
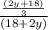
=
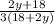
Ratio of P₁ and P₂ = (
 ) ⇒ P₂ = 3P₁
) ⇒ P₂ = 3P₁
Therefore, Option a is the answer.