Question

A mixing blade on a food processor extends out 3 inches from its center. if the blade is turning at 600 revolutions per minute, what is the linear velocity of the tip of the blade in feet per minute? (round your answer to the nearest whole number.)

Answer 1

The linear velocity of the tip of the blade is 940.94 ft/min.

Step-by-step explanation:

It is given that,

A mixing blade on a food processor extends out 3 inches from its center, r = 3 inches = 0.0762 meters

Angular speed of the blade,
`\omega=600\ rev/minute=62.83\ rad/s`

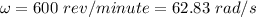
Let v is the linear velocity of the tip of the blade. The relation between the angular velocity and the linear velocity is given by :

`v=r* \omega`

`v=0.0762* 62.83`

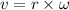
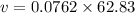
v = 4.78 m/s

or

Since, 1 m/s = 196.85 ft/min

4.78 m/s = 940.94 ft/min

So, the linear velocity of the tip of the blade is 940.94 ft/min. Hence, this is the required solution.

Answer 2

First let's convert everything into SI units.
The length of the blade is 3 inches. Keeping in mind that 1 inc=0.025 m, we have

`L=3 in \cdot 0.025 (m)/(inc) =0.075 m`
The angular speed is 600 revolutions per minute. Keeping in mind that
`1 rev=2 \pi rad` and
`1 min=60 s`, the angular speed becomes

`\omega = 600 (rev)/(min) (2 \pi rad/rev)/(60 s/min)=62.8 rad/s`

And so, the linear velocity of the edge of the blade is equal to

`v=\omega L=(62.8rad/s)(0.075 m)=47 m/s`