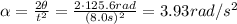Question

A grindstone, initially at rest, is given a constant angular acceleration so that it makes 20.0 rev in the first 8.00 s. what is its angular acceleration?

Answer 1

The angle covered by the grindstone during this time is, converting into radians,

`\theta = 20 rev = 20 rev \cdot (2 \pi rad)/(rev) =125. 6rad`

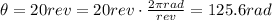
This is a rotational motion with constant angular acceleration
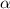
`\alpha`, and with initial angular speed
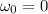
`\omega _0 =0`. The angle covered in a time t is given by

`\theta (t)= \omega_0 t+ (1)/(2) \alpha t^2 = (1)/(2) \alpha t^2`
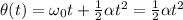
because the initial angular speed is zero.
Using t=8.00 s, we can find the value of angular acceleration:

`\alpha = (2 \theta)/(t^2)= (2 \cdot 125.6 rad)/((8.0 s)^2)=3.93 rad/s^2`