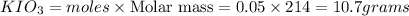Answer: The masses of
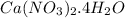 and
and
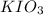 required to make 10.0 g of
required to make 10.0 g of
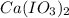 is 5.9 and 10.7 grams respectively.
is 5.9 and 10.7 grams respectively.
Explanation: To calculate the moles, we use the equation:
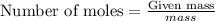
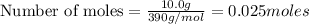
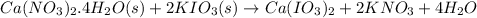
1 mole of
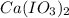 is formed from 1 mole of
is formed from 1 mole of
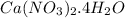 and 2 moles of
and 2 moles of
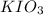
Thus 0.025 moles of
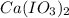 is formed from 0.025 moles of
is formed from 0.025 moles of
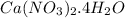 and 0.05 moles of
and 0.05 moles of
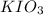
Mass of
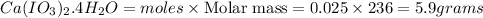
Mass of