Question

Calculate the height of a cuboid which has a base area of 180 cm2 and volume is 900 cm3


`help`
​

Answer 1

Height of the Cuboid = 5 cm

Explanation:

`\bf \: Given:`

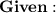
Base area = 180 cm²

Volume = 900 cm³

`\bf \: To \: find :`

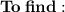
The height of the cuboid

`\bf \: Solution:`

We know that ,

`\boxed{\sf \: Volume \: of \: Cuboid = base \: area * height}`

`\rm \: S o,put \: the \: values :`

`\sf \implies 900 = 180 * height`

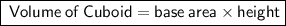
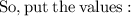
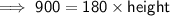
This is an equation which will help in finding the value of height.

Note: The answer would be in cm.

`\bf \: Solve \: this \: equation.`

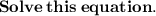
Change their respective sides :

`\sf \implies \: height *180 = 900`

Now,

`\sf \implies{height} = \cfrac{900}{180}`

Cancel a zero of 900 and a zero 180:

`\sf \implies{height} = \cfrac{90 \cancel0}{ 18\cancel0}`

`\sf \implies \: height = \cfrac{ 90}{18}`

Cancel 90 and 18 :

`\sf \implies{heigh}t = \cfrac{ \cancel{{90}}^5}{ \cancel{{18}} ^1 }`

`\sf \implies height = 5 \: cm`

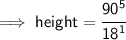
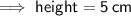
Hence, the height of the cuboid would be 5 cm .

`\rule{225pt}{2pt}`

I hope this helps!