Question

The points (6, -2) and (h, -3) fall on a line with a slope of 1/3. What is the value of h?

Answer 1

17/3

Step-by-step explanation:

Make it into a fraction like

6-h/-2+3 = 1/3

this equals 6-h/1=1/3

18-3h=1

-18 -18

-3h=17

/-3 /-3

h=17/3

Cannot simplify

h=17/3

Answer 2

Answer: h = 3

======================================================

Work Shown:

m = 1/3 is the given slope

We'll use the slope formula to solve for h.

`(x_1,y_1) = (6,-2) \text{ and } (x_2,y_2) = (h,-3)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\(1)/(3) = (-3 - (-2))/(h - 6)\\\\(1)/(3) = (-3 + 2)/(h - 6)\\\\(1)/(3) = (-1)/(h-6)\\\\1(h-6) = 3(-1)\\\\h-6 = -3\\\\h = -3+6\\\\h = 3`

-----------------------------

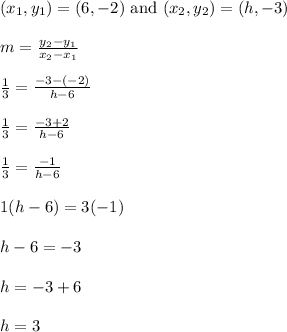
Let's check the answer.

The point (h,-3) updates to (3,-3)

The claim is that the points (6,-2) and (3,-3) fall on a line with slope 1/3.

Use the slope formula to get the following:

`(x_1,y_1) = (6,-2) \text{ and } (x_2,y_2) = (3,-3)\\\\m = (y_(2) - y_(1))/(x_(2) - x_(1))\\\\m = (-3 - (-2))/(3 - 6)\\\\m = (-3 + 2)/(3 - 6)\\\\m = (-1)/(-3)\\\\m = (1)/(3)\\\\`

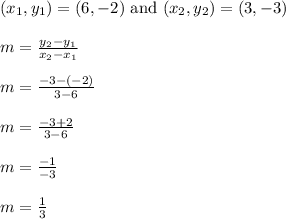
We get a slope of 1/3 as expected.

The answer is confirmed.

A slope of 1/3 means that each time you move up 1 unit (rise), move to the right 3 units (run).