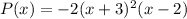The polynomial is of the form:
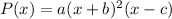
We are provided with the two zeros in the question statement. The zero with multiplicity 2 is -3, and zero with multiplicity 1 is 2. So using these values, the polynomial becomes:
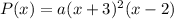
The polynomial also passes from the point (0,36). This mean if we substitute x=0, the answer should be 36.

Thus the value of a for given polynomial will be -2. The complete equation of polynomial will be: