Question

Factor completely. a2+3a−28 Enter your answer in the box.

Answer 1

By a2, I assume you mean a squared. If so, then the answer is (x+7)*(x-4).

Answer 2

To factor completely

`a^(2) + 3a-28`

To factor it completely , first take the product of first and third term, and then break the second term in two parts in such a way that its sum equals the second term and the product equals the product of first and third term.

Product of first and third term is
`(a^(2))(-28) = -28 a^(2)`

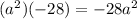
Second term is 3a, Re-write 3a as sum of 7a and -4a.

Lets check it Product of 7a and -4a is
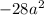`-28 a^(2)` wich is eaqual to product of first and third term and sum of 7a and -4a is 3a which is the second term.

Now factorise, we get

`a^(2)+3a-28\\\\ = a^(2) +7a-4a-28\\\\=a(a+7)-4(a+7)\\\\=(a+7)(a-4)`

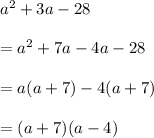
Hence,
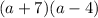`(a+7)(a-4)` is the factor of
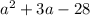`a^(2)+3a-28`.