Question

Helppppppppppppppppppppp

Answer 1

The composition of a function and its inverse is x. So an easy approach to solve this question is to find the composition of a function with itself. If the composition results in an answer "x", then this will mean that function and its inverse are the same.

Finding the composition for 1st option:

`(fof)(x) = f(f(x))= ( (x-1)/(x+5)-1 )/( (x-1)/(x+5)+5 ) \\ \\ = ( (x-1-x-5)/(x+5) )/( (x-1+5x+25)/(x+5) ) \\ \\ = (-6)/(6x+24) \\ \\ = (1)/(x+4)`

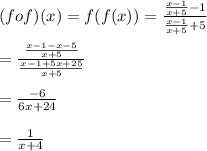
Since the composition of the function with itself is not x, the function and its inverse are not the same.

Similarly, we can find the compositions of next 3 functions with themselves. The results of compositions are listed below:

(gog)(x)=g(g(x)) = x

(hoh)(x)=h(h(x))=
`(4x-3)/(7-x)`

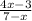
(kok)(x)=k(k(x))= x

Thus the option 2 and 4 are the correct answers i.e. these functions are the same as their inverse functions.