Question

Which shows one way to determine the factors of x3 – 9x2 + 5x – 45 by grouping?

Answer 1

x(x2 + 5) – 9(x2 + 5)

Explanation:

Answer 2

Factoring by grouping usually pairs up the first 2 sets of expressions with the second 2 sets. Ours looks like this, then:
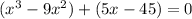
`(x^3-9x^2)+(5x-45)=0`. If we factor out the common x-squared in the first set of parenthesis, along with factoring out the common 5 in the second set, we get this:
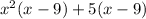
`x^2(x-9)+5(x-9)`. Now the common expression that can be factored out is the (x-9). When we do that, here's what it looks like:
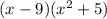
`(x-9)(x^2+5)`. I'm not sure how far you are going with this. You could set each of those equal to 0 and solve for x in each case. The first one is easy. If x - 9 = 0, then x = 9. The second one involves the imaginary i since x^2 = -5. In that case,
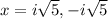
`x=i √(5),-i √(5)`. Hopefully, in what I have given you, you can find what you're looking for.