Question

How much compound interest is earned on $2050 at 4% interest for 3 years, compounded annually? Give your answer in dollars and cents. Don’t forget to subtract P from A.

Answer 1

$255.97 is the correct answer

Answer 2

To solve for the amount + interest for compounding interest you will use this formula:

`A = P ( 1 + (r)/(n)) ^(nt)`

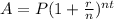
Where A = Accrued amount
P = Principal amount
r = rate in decimal
t = number of years
n = compounding periods per unit of time
Your given:
P = $2050
r = 4% or 0.04
t = 3 years
n = 1 per yr
Now we insert that into your formula:

`A = P ( 1 + (r)/(n)) ^(nt)`

`A = 2050 ( 1 + (0.04)/(1)) ^(1.3)`

`A = 2050 ( 1 + 0.04) ^(3)`

`A = 2050 ( 1.04) ^(3)`

`A = 2050 (1.124864 )`

`A = $2305.97`

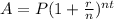
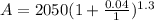
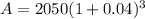
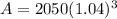
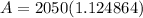
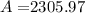
Now to get the interest just remember that:
I = A - P
I = $2,305.97 - $2,050
I = $255.97
So that is equal to 255 dollars and 97 cents