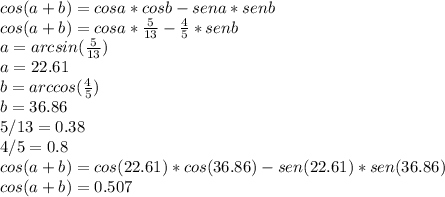Answer:
cos(a+b)≈0.507
Explanation:
Hi there, in Quadrant I both sine and cosine functions are positive.
This cos (a+b) being a Classical Trigonometrical Identity, the product of the sum between two cosines equals the product of two cosines minus the product of two sines.
But we need to find the value of a and b, so that we can go on. Calculate the arccosine and arcsine function respectively is mandatory