Answer:
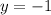
Explanation:
We have been given an equation of parabola
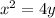 . We are asked to find the directrix of our given parabola.
. We are asked to find the directrix of our given parabola.
First of all, we will divide both sides of our given equation by 4.
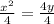
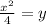
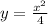
Now, we will compare our equation with vertex form of parabola:
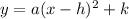 , where, (h,k) represents vertex of parabola.
, where, (h,k) represents vertex of parabola.
We can see that the value of a is
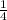 ,
,
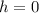 and
and
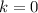 .
.
Now, we will find distance of focus from vertex of parabola using formula
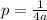 .
.
Substituting the value of a in above formula, we will get:
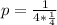
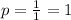
We know that directrix of parabola is
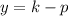 .
.
Substituting the value of k and p in above formula, we will get:
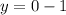
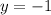
Therefore, the directrix of our given parabola is
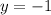 .
.