Question

A playground is being designed where children can interact with their friends in certain combinations.

If there is 1 child, there can be 0 interactions.
If there are 2 children, there can be 3 interactions.
If there are 3 children, there can be 12 interactions.
If there are 4 children, there can be 39 interactions.

Which recursive equation represents the pattern?

an = an – 1 + 3(n – 1)

an = an – 1 + 3(n – 1)

an = an – 1 + (3n – 1)

an = an – 1 + (n – 1)3

Answer 1

From your situations given:
If there is 1 child, there can be 0 interactions.
If there are 2 children, there can be 3 interactions.
If there are 3 children, there can be 12 interactions.
If there are 4 children, there can be 39 interactions.

The equation would be an = an – 1 + 3(n – 1)

Answer 2

`a_n=a_(n-1)+3^(n-1)`

Explanation:

It is given that

If there is 1 child, there can be 0 interactions.

If there are 2 children, there can be 3 interactions.

If there are 3 children, there can be 12 interactions.

If there are 4 children, there can be 39 interactions.

It means we have,

`a_1=0, a_2=3, a_3=12, a_4=39`

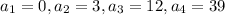
We need to find the recursive equation that represents the pattern.

`a_2=3\Rightarrow 0+3=a_1+3`

`a_3=12\Rightarrow 3+9=a_2+3^2`

`a_4=39\Rightarrow 12+27=a_3+3^3`

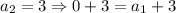
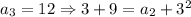
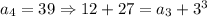
Similarly,

`a_n=a_(n-1)+3^(n-1)`

Therefore, the required recursive formula is
`a_n=a_(n-1)+3^(n-1)`.