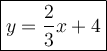Question

What is an equation of the line that passes through the points (6, 8) and (−3,2)?

Answer 1

Step-by-step explanation

• Calculate the slope by using rise over run with two given coordinate points.

`m = (8 - 2)/(6 - ( - 3)) \\ m = (6)/(6 + 3) \\ m = (6)/(9) \\ m = (2)/(3)`

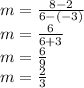
The slope is 2/3.

• Slope-intercept form

`y = mx + b`

where m = slope and b = y-intercept. Substitute the value of m in slope-intercept form.

`y = (2)/(3) x + b`

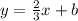
• Substitute one of two coordinate points in the slope-intercept form.

I will use (-3,2) instead.

`2 = (2)/(3) ( - 3) + b \\ 2 = - 2 + b \\ 2 + 2 = b \\ 4 = b`

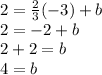
The y-intercept is (0,4). Then rewrite the equation by substituting the b-value and slope in slope-intercept form.

`y = (2)/(3) x + 4`

Answer

`\large \boxed{y = (2)/(3) x + 4}`