In order to find a horizontal asymptote of a function f(x), you need to calculate
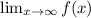
= n
where n is a finite number.
in your case you have to caculate separately the two limits:
a)
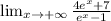
=
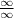
To solve this, you need to regroup eˣ both on the numerator and on the denominator:
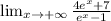
=
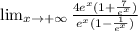
At this point the two e
ˣ cancel out and the parenthesis tend to 1, therefore
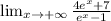 = 4
= 4
Your first horizontal asymptote is y = 4.
b) Let's calcuate now:
 =
=
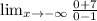 = -7
= -7
Therefore your second horizontal asymptote is y = -7
Your answer is, hence, y = 4 and y = -7 are horizontal asymptotes of the given function.