Answer: 0.23 grams
Step-by-step explanation:
According to avogadro's law, 1 mole of every substance weighs equal to its molecular mass and contains avogadro's number
 of particles.
of particles.
To calculate the number of moles, we use the equation:
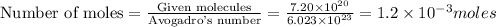
1 mole of caffeine
 weighs = 194 g
weighs = 194 g
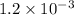 moles of
moles of
 weigh =
weigh =

Thus mass of caffeine
 is 0.23 grams.
is 0.23 grams.