Question

Solve the triangle.

A = 48, a = 32, b = 27

I am completely blanking on how to do this, so if you could please do a step by step process, that would be greatly appreciated :)

Answer 1

The triangle is A = 48°, a = 32, B = 38.83°, b = 27, C = 93.17° and c = 42.99

Explanation:

We have sine rule,

`(a)/(sinA)=(b)/(sinB)=(c)/(sinC)`

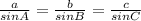
Here given A = 48°, a = 32, b = 27

Substituting

`(32)/(sin48)=(27)/(sinB)=(c)/(sinC)\\\\sinB=0.627\\\\B=38.83^0`

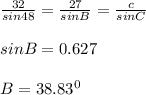
We have

A + B + C = 180°

48 + 38.83 + C = 180

C = 93.17°

Using sine rule again

`(32)/(sin48)=(c)/(sin93.17)\\\\c=42.99`

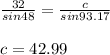
So the triangle is A = 48°, a = 32, B = 38.83°, b = 27, C = 93.17° and c = 42.99

Answer 2

32/sin 48 = 27/sin B or
sin B = (27/32)*sin 48 = 0.6270 or
B = 39°; C=180-48-39 = 93°
c^2 = a^2 +b^2 -2abcos C = 32^2 +27^2 -{2*32*27*cos 93}=1843 or
c =43