Question

The charge within a small volume dv is dq=ρdv. the integral of ρdv over a cylinder of length l is the total charge q=λl within the cylinder. use this fact to to determine the constant ρ0 in terms of λ and r. hint: let dv be a cylindrical shell of length l, radius r, and thickness dr. what is the volume of such a shell?

Answer 1

Given

dq=density*dv

q=lamda*I

Taking double integration

density=lamda/2*pi*r^2

Answer 2

The volume of the shell that you described would be:

`dV=2L\pi r dr`
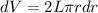
Now we can rewrite the given integral:

`\lambda L=\int\rho dV=L\rho\int2\pi r dr \\ \lambda L =L\rho \pi r^2\\ \rho=(\lambda)/(\pi r^2)`
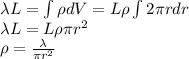
I have attached the picture explaining how we got the formula for the volume.
On the picture, I marked the rectangle. You can of this rectangle as the base, and the height would be the circumference of the cylinder.