Question

How much work does an elevator motor do to lift a 1200-kg elevator car a height of 80 m at constant speed?

Answer 1

Work = 940800 J

Step-by-step explanation:

As we know that work done is defined as

Work = (Force)(displacement in the direction of force)

here elevator motor lift a mass of 1200 kg

so in order to lift it up motor must have to apply the force same as the weight so that it will move up with constant speed.

so here we have

`F = mg`

`F = (1200 kg)(9.8 m/s^2)`

`F = 11760 N`

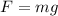
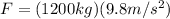
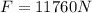
now it is displaced upwards by distance d = 80 m

so here we have

`W = (11760)* (80)`

`W = 940800 J`

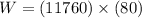
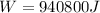
so above is the work done by the elevator to lift it upwards

Answer 2

The increase in gravitational potential energy of the elevator car when is lifted to a height of 80 m is given by

`\Delta U=mg \Delta h`
where m=1200 kg is the mass of the elevator car,
`g=9.81 m/s^2` is the gravitational acceleration, and
`\Delta h=80 m` is the variation of height of the elevator car. If we plug these numbers into the equation, we find:

`\Delta U=(1200 kg)(9.81 m/s^2)(80 m)=9.42 \cdot 10^5 J`

For the work-energy theorem, the work done by the motor to lift the elevator must be equal to the energy acquired by the elevator car: but the energy acquired by the elevator car is
`9.42 \cdot 10^5 J`, therefore the work done by the motor is exactly equal to this value:

`W=\Delta U=9.42 \cdot 10^5 J`