Question

The vertices of quadrilateral abcd are a(1, a - 3), b(10, a), c(9, a + 3) and d(0, a).prove that the quadrilateral is a rectangle.find the midpoints of the diagonals.the midpoint of ac is (5,1)the midpoint of bd is (5,1)find the lengths of the diagonals.

Answer 1

sorry fam im stumped hope you get the answer your looking for

Answer 2

Answer with explanation:

The Vertices of quadrilateral A B CD, are A(1, a - 3), B(10, a), C(9, a + 3) and D(0, a).

Mid point of AC= (5,1)

Mid point of B D= (5,1)

Mid point formula of two points having coordinates , (a,b) and (c,d) is , if (x,y), then

`x=(a+b)/(2),y=(c+d)/(2)`

`So,\rightarrow (a-3+a+3)/(2)=1\\\\\rightarrow (2a)/(2)=1\\\\\rightarrow a=1`

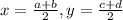
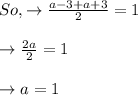
So, the coordinates of vertices of quadrilateral A B CD, are A(1, -2), B(10, 1), C(9, 4) and D(0, 1).

Distance formula of two points having coordinates, (a,b) and (c,d) is,

`=√((a-c)^2+(b-d)^2)`

`AB=√((10-1)^2+(1+2)^2)=√(81+9)=√(90)=3√(10)\\\\BC=√((10-9)^2+(1-4)^2)\\\\=√(1+9)\\\\=√(10)\\\\CD=√((9-0)^2+(3-0)^2)=√(90)=3√(10)\\\\DA=√((1-0)^2+(1+2)^2)=√(10)\\\\AC=√((9-1)^2+(4+2)^2)=√(64+36)\\\\AC=√(100)\\\\AC=10\\\\BD=√((10-0)^2+(1-1)^2)\\\\BD=10`

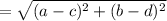
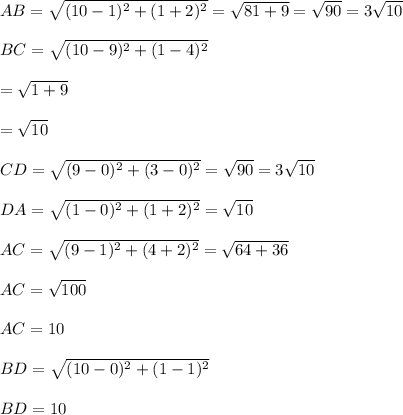
Opposite sides AB and CD are equal to 3√10 unit and , BC and AD are equal to √10 unit.

Also,length of Diagonals , AC=B D=10 unit.

∴ The Quadrilateral, AB CD is a Rectangle.