Solution:
we are given that
The population of a city in 2005 was 18000.
By 2010, the city’s population had grown to 45,000.
Economists have determined that the growth is exponential.
As we know the exponential growth is defined by the relation
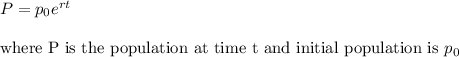
Here we have
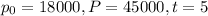
substitute these values we get
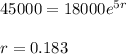
So we get
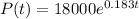
So For population is 2015 substitute t=10
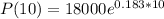
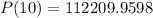
The projected population for 2015 is 112210