Question

WORTH 30 PTS PLS ANSWER ASAP.

Jordan is a manager of a car dealership. He has two professional car washers, Matthew and Arianna, to clean the entire lot of cars. Matthew can wash all the cars in 14 hours. Arianna can wash all the cars in 11 hours. Jordan wants to know how long it will take them to wash all the cars in the lot if they work together.

Write an equation and solve for the time it will take Matthew and Arianna to wash all the cars together. Explain each step.

Answer 1

Assuming that X represents the number of hours worked and f(x) the number of cars washed, the equation would be f(x)=11x+14x.

The 11x represents the number of cars washed by Arianna in x number of hours and the 14x represents the number of cars washed by Matthew in x number of hours. You add the two because they are each washing their own car at their own pace but working on one lot.

Answer 2

They will take 6.16 hrs or 6 hrs, 9 minutes and 36 seconds.

Explanation:

Consider the provided information.

Let x is the number of cars in a lot.

Matthew can wash all the cars in 14 hours. That means in 1 hr he can wash x/14 cars.

Arianna can wash all the cars in 11 hours. That means in 1 hr Aranna can wash x/11 cars.

Together there rate will be:

`(x)/(14)+(x)/(11)=(x)/(y)`

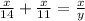
Here y represent the time taken by them if they work together.

Divide both sides by x, we get

`(1)/(14)+(1)/(11)=(1)/(y)`

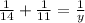
Thus, the required equation is:
`(1)/(14)+(1)/(11)=(1)/(y)`

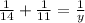
Now solve for time, Here time is represents by y.

`(1)/(14)+(1)/(11)=(1)/(y)`

`(11+14)/(154)=(1)/(y)`

`(25)/(154)=(1)/(y)`

`y=(154)/(25)`

`y=6.16`

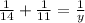
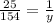
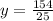
Hence, they will take 6.16 hrs or 6 hrs, 9 minutes and 36 seconds.