Question

The integral of: -xe^x²

Answer 1

`I = \int-xe^(x^2) dx`

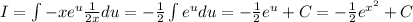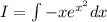
Notice this integral has
`x^2` and
`x` in it. Since
`(d)/(dx)(x^2)=2x` this means we can use substitution to make this integral much simpler.

PRO-TIP: If an integral contains both some function of x, f, and it's derivative
`(df)/(dx)`. Choose u=f(x).

In our case we choose
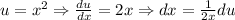
`u=x^2 \Rightarrow (du)/(dx) = 2x \Rightarrow dx = (1)/(2x) du`. So the integral becomes
`I= \int -xe^u (1)/(2x) du= -(1)/(2) \int e^u du = -(1)/(2) e^u +C = -(1)/(2) e^(x^2) +C`