Let us calculate the average energy of a molecule at such a temperature. The formula that gives it is E=3/2(kT) where k is the Boltzmann constant and T is the temperature in Kelvin. This formula holds for atoms, not substances with 2 or more atoms, but it is a good approximation (same order of magnitude) for other cases too. T=15+273=288K and k=1.38 × 10^(-23) J/K. Substituting, the energy is 3.97*10^(-21) Joules. The kinetic energy of an atom is also:
E=(1/2)mv*v where v is its speed and m is its mass. We know the speed, we are given to assume that it is the escape velocity and we have calculated E. Solving for m, we get:
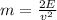
. Substituting we have that m=6.34*10^(-27) kg.
We now have to look up some mass values at a table. The most characteristic one is the mass of the hydrogen atom which is around 1.68*10^(-27) kg. We have thus that the mass of the hydrogen atom is lower than what we calculated. The mass of the He atom has around 4 times the mass, so it is around 6.7*10^(-27) kg. We thus have that the hydrogen atoms have a speed higher than the escape velocity due to their thermal motion (their mass is below the threshold that we calculated). A lot of helium atoms must be gone from the atmosphere too since the value of the mass is very close to the threshhold; if the temperature was 30C then helion could possibly leave the atmosphere. Finally, argon is much heavier than both these elements and hence its speed is going to be much smaller
(mass is inversely proportional to the square of the speed when the temperature is constant). Hence, we expect a lot of the argon that was initially in the atmosphere to have stayed.