Question

Evaluate sin[2 arccos( -8/17 )].

Answer 1

Recall that
`\sin2x=2\sin x\cos x`, so that


`\sin\left(2\arccos\left(-\frac8{17}\right)\right)=2\sin\left(\arccos\left(-\frac8{17}\right)\right)\cos\left(\arccos\left(-\frac8{17}\right)\right)`

Dealing with the cosine terms is simple, since
`\cos(\arccos x)=x` (so long as
`0\le \arccos x\le\pi`, which is true here). So


`\cos\left(\arccos\left(-\frac8{17}\right)\right)=-\frac8{17}`

To find the sine, we can make a substitution of
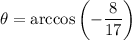
`\theta=\arccos\left(-\frac8{17}\right)`. In other words, we suppose that
`\theta` is some angle that satisfies
`\cos\theta=-\frac8{17}`.

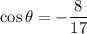
If this is the case, then we have


`\sin^2\theta=1-\cos^2\theta=(225)/(289)\implies\sin\theta=\pm\sqrt{(225)/(289)}=\pm(15)/(17)`

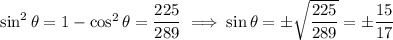
But which value do we choose? We know that
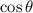
`\cos\theta` is negative, which means
`\theta` must be between
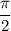
`\frac\pi2` and
`\pi`. The sine of any angle
`\theta` in this interval will always be positive, so in fact


`\sin\theta=\sin\left(\arccos\left(-\frac8{17}\right)\right)=(15)/(17)`

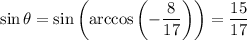
Putting everything together, we get


`\sin\left(2\arccos\left(-\frac8{17}\right)\right)=2\left((15)/(17)\right)\left(-\frac8{17}\right)=-(240)/(289)`