Question

Part 1.] Does the graph have even symmetry, odd symmetry, or neither?

Part 2.] Does the graph of y = sin x have even symmetry, odd symmetry, or neither?

Part 3.] Identify the transformations that describe the graph of an even function. Select all that apply.

reflection over the x-axis; 

reflection over the y-axis;  reflection over the line y=x;  90° rotation around the origin;  180° rotation around the origin

Answer 1

Part 1
The graph has even symmetry. You can see that because it is symmetric with respect to the y-axis.
Functions that have even symmetry have the following property:

`f(x)=f(-x)`
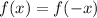Part 2
To answer this we can simply check if the property we mentioned earlier holds for this function.

`sin((\pi)/(2))\\e sin(-(\pi)/(2))`
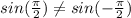
We can see that sine does not have even symmetry.
In fact, sine function has the following property:

`sin(x)=-sin(x)`
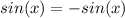
This is called odd symetry.
Part 3
Take a look at the function that you attached in the picture. We know that function has even symmetry.
Reflection over x-axis and 180° rotation around the origin would give us -f(x). We would not end up with the same function, so these two are out.
90° rotation around the origin would mean we swapped x and y so that one is out too. Reflection over the line y=x is a property of functions that have an odd symmetry.
We are left with reflection around y-axis and, as mentioned before, this is the property of evenly symmetric functions.