Question

What is the approximate solution of this system of equations?

y = x2 + 3x + 3
y = x2 + x + 2

(-0.5, 0.2)
(-0.5, 1.7)
(-0.1, 1.2)
(0.2, 1.5)

Answer 1

I believe it's the second one, (-0.5, 1.7)


Comment the correct answer.

Answer 2

(B)

Explanation:

The given system of equations are:

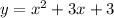`y=x^2+3x+3` (1)

and
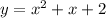`y=x^2+x+2` (2)

Subtracting equation (2) from (1), we get

`0=2x+1`

⇒
`2x=-1`

⇒
`x={(-1)/(2)}`

⇒
`x=-0.5`

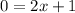
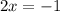
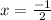
Now, substituting the value of x=-0.5 in equation (2), we get

`y=0.25-0.5+2`

⇒
`y=1.7`

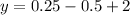
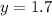
Thus, the values of x and y are -0.5 and 1.7.

Therefore, the approximate solution of the given system of the equation is (-0.5, 1.7).

Hence, option (B) is correct.