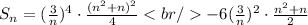Question

Express the given integral as the limit of a riemann sum but do not evaluate: the integral from 0 to 3 of the quantity x cubed minus 6 times x, dx.

Answer 1

We will use the right Riemann sum. We can break this integral in two parts.

`\int_(0)^(3) (x^3-6x) dx=\int_(0)^(3) x^3 dx-6\int_(0)^(3) x dx`
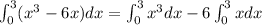
We take the interval and we divide it n times:

`\Delta x=(b-a)/(n)=(3)/(n)`
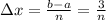
The area of the i-th rectangle in the right Riemann sum is:

`A_i=\Delta xf(a+i\Delta x)=\Delta x f(i\Delta x)`
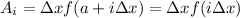
For the first part of our integral we have:

`A_i=\Delta x(i\Delta x)^3=(\Delta x)^4 i^3`
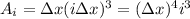
For the second part we have:

`A_i=-6\Delta x(i\Delta x)=-6(\Delta x)^2i`
We can now put it all together:

`\sum_(i=1)^(i=n) [(\Delta x)^4 i^3-6(\Delta x)^2i]\\\sum_(i=1)^(i=n)[ ((3)/(n))^4 i^3-6((3)/(n))^2i]\\ \sum_(i=1)^(i=n)((3)/(n))^2i[((3)/(n))^2 i^2-6]`
We can also write n-th partial sum:

`image`