Question

Find a linear differential operator that annihilates the given function. (use d for the differential operator.) e−x + 8xex − x2ex

Answer 1

Answer:
`(d - 1)^3(d + 1)`

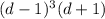
Step-by-step explanation:

Let


`f(x) = e^(-x) + 8xe^x - x^2 e^x`.

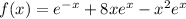
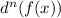
`d^n (f(x))` = nth derivative of f

Note that


`(d + 1) (e^(-x)) = d (e^(-x)) + e^(-x) = -e^(-x) + e^(-x) = 0 \\ \boxed{\Rightarrow (d + 1)e^(-x) = 0}`

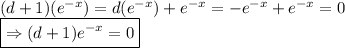
So, (d + 1) annihilates
`e^(-x)`.

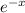
Note that


`(d + 1) (8x e^x - x^2 e^x) = d(8x e^x - x^2 e^x) + (8x e^x - x^2 e^x) \\ = (8e^x + 8x e^x - 2x e^x - x^2 e^x) + (8x e^x - x^2 e^x) \\ \boxed{(d + 1) (8x e^x - x^2 e^x) = 8e^x + 14x e^x - x^2 e^x}`

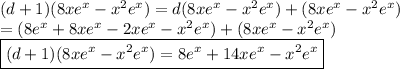
Let
`g(x) = 8e^x + 14x e^x - x^2 e^x`

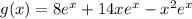
For any real number
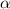
`\alpha` and positive integer n,


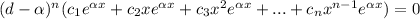
`(d - \alpha)^n (c_1 e^(\alpha x) + c_2 xe^(\alpha x) + c_3 x^2 e^(\alpha x) + ... + c_n x^(n - 1) e^(\alpha x)) = 0` (1)

So, for g(x),
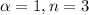
`\alpha = 1, n = 3`. Thus, using equation (1),


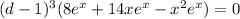
`(d - 1)^3 (8e^x + 14x e^x - x^2 e^x) = 0` (2)

Since,
`8e^x + 14x e^x - x^2 e^x = (d + 1) (8x e^x - x^2 e^x)` ,


`(d - 1)^3 ((d + 1) (8x e^x - x^2 e^x)) = (d - 1)^3 (8e^x + 14x e^x - x^2 e^x) = 0`

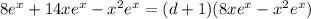
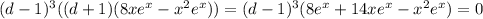
Moreover, since
`(d + 1) (e^(-x)) = 0`


`(d - 1)^3(d + 1) (e^(-x)) = (d - 1)^3 (0)`

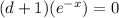
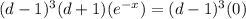
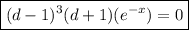
`\\ \boxed{(d - 1)^3(d + 1) (e^(-x)) = 0 }` (3)

Hence based on equations (2) and (3),


`(d - 1)^3(d + 1) (e^(-x) + 8xe^x - x^2e^x) \\ = (d - 1)^3(d + 1)(e^(-x)) + (d - 1)^3(d + 1)(8xe^x - x^2e^x) \\ = 0 + 0 \\ \boxed{(d - 1)^3(d + 1) (e^(-x) + 8xe^x - x^2e^x) = 0}`

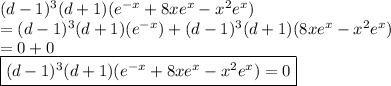
Therefore, the linear operator
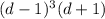`(d - 1)^3(d + 1)` annihilates
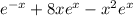`e^(-x) + 8xe^x - x^2e^x`.