Question

Find three positive consecutive integers such that the product of the second integer and the third integer is 72

Answer 1

Let xbe a positive integer number. Then x, x+1 and x+2 are three positive consecutive integers (the first one is x, the second is x+1 and the third is x+2).

The product of the second integer and the third integer is (x+1)·(x+2) and is equal to 72. So you have the equation

`(x+1)\cdot (x+2)=72.`

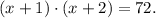
Solve it:

`x^2+2x+x+2=72,\\ \\x^2+3x+2-72=0,\\ \\x^2+3x-70=0,\\ \\D=3^2-4\cdot (-70)=9+280=289,\\ \\√(D)17,\\ \\x_1=(-3-17)/(2)=-10,\ x_2=(-3+17)/(2)=7.`

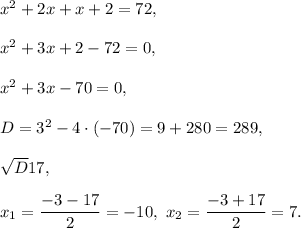
Solution
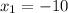`x_1=-10` is extra because
`x_1` is negative.

Answer: three positive consecutive integers are 7, 8 and 9.

Answer 2

Let
x---------> first positive integer
x+1------> second positive integer
x+2-----> third positive integer

we know that
(x+1)*(x+2)=72-------> x² +2x+x+2=72 -------> x² +3x-70=0

using a graph tool-------> I solve the quadratic equation
see the attached figure

the roots are
x1=-10
x2=7

the answer is
first positive integer is x=7
second positive integer is x+1=8
third positive integer is x+2=9