Question

The sum of two numbers is 44. One number is 3 times as large as the other. What are the numbers?

Answer 1

let one of the number be x

one number = x
the other number = 3x

Given that the sum of these two number is 44.
x + 3x = 44
4x = 44
x = 44 ÷ 4
x = 11

x = 11
3x = 11 x 3 = 33

The two numbers are 11 and 33

Answer 2

Set up 2 variables:
x = larger number
y = smaller number

Set up equations:

`x + y = 44`

`3y = x`

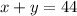
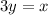
Solve by substituting. I will use the x already given to us (in second equation) to substitute in 1st equation (x = 3y):

`3y + y = 44`

`4y = 44`

`y = 11`

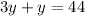
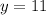
Plug it back into 2nd equation to solve for x:

`3y = x`

`3(11) = x = 33`

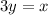
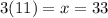
So, our two values are: x = 33 and y = 11.

We can check, x + y = 33 + 11 does equal 44 and 33 times is 3 times larger than 11. So, the initial criteria work out and we are right.