Answer:
For
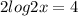 , x = 50
, x = 50
Step-by-step explanation:
Given :
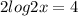
We have to find the value of x.
Consider the given
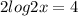
Divide both side by 2, we have,
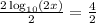
Simplify, we have,
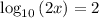
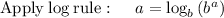
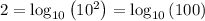
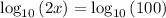
When log have same base, we have,
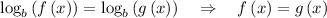
We have,
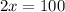
Divide both side by 2, we have,
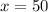
Thus, For
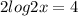 , x = 50
, x = 50