Answer:
b.) The graph's x-intercepts are similar to ½(x - 5)(x + 2).
a.) [-2, 0], [5, 0]
__________________________________________________________
b.) The graph has a maximum value because the graph opens down [-2 = A].
a.) [-3, -4]
__________________________________________________________
d) [0, -5]
c) -2 = x
b) [-2, -9] → [h, k]
a) -1, 5 = x
Step-by-step explanation:
b) Both graphs have the binomial of [x - 5][x + 2], so the x-intercepts never altered.
a) Set the binomial equal to zero, and you will get your x-intercepts of [-2, 0] and [5, 0].
__________________________________________________________
b) When A is negative, your graph will have a maximum value [opens down], whereas when A is positive, your graph will have a minimum value [opens up].
a) According to the Vertex Formula, y = A[X - H]² + K, [H, K] represents the vertex, plus, -H gives you the OPPOSITE TERMS OF WHAT THEY REALLY ARE, so be EXTREMELY CAREFUL labeling your vertex. Additionally, K gives you the NORMAL TERMS.
__________________________________________________________
d) The y-intercept is your C-term, so in this case, it is [0, -5].
c) To find the axis of symmetry, use this formula:
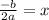
Whatever the opposite of your B-term is, you take that and divide it by twice your A-term.
b) To find the vertex, in this case, you have to go from Standard Form to Vertex Form by completing the square, using this formula to get part of your new C-term:
![[(b)/(2)]^(2)](https://img.qammunity.org/2019/formulas/mathematics/high-school/kgyrvuaq0r8a2hwadpggucooslr2yfwbn4.png)
When done, you get this:
![y = {x}^(2) + 4x + 4 \\ \\ y = [x + 2]^(2)](https://img.qammunity.org/2019/formulas/mathematics/high-school/bw1dj9n003ghfb3kxl68vwf28uvdg000d0.png)
Then, you have to deduct some number from 4 that gave you -5 in the first place, and that integer is -9. So, here is the result:
![y = [x + 2]^(2) - 9](https://img.qammunity.org/2019/formulas/mathematics/high-school/os0ght4uwkeprdz64sqid34rr517c16iwh.png)
From here, we can see that our vertex is [-2, -9].
a) When the binomial is set to equal to zero, you get this:
![{x}^(2) + 4x - 5 \\ \\ [x - 1][x + 5] = 0 \\ \\ 1, \: -5 = x](https://img.qammunity.org/2019/formulas/mathematics/high-school/azxop3cqst8dx6xnrhfyheilzj3esollco.png)
e) See above photograph
I am joyous to assist you anytime.