Question

John and Matt are going to fill a pool with 2 different sized hoses. John can fill the pool in 5 hours, while Matt can complete it in 10 hours. Explain each step in solving this equation. (10 points)

Answer 1

We have to find how much time will be consumed if both John and Matt fill the pool together and show the steps to reach at the answer.

Solution:

John fill the pool in 5 hours. This means in 1 hour John fills
`(1)/(5)` part of the pool. Matt fills the pool in 10 hours. This means in 1 hour Matt fill
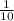
`(1)/(10)` part of the pool.

If they both work together:
Portion of the pool filled in 1 hour =
`(1)/(5)+ (1)/(10)= (3)/(10)`

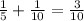
Next we can use proportion to solve this problem.

3/10 portion of the pool is filled in 1 hour.

3/10 of the pool is filled in time ⇒ 1 hour
Multiplying both sides by 10/3 we get

3/10 x 10/3 of the pool in time = 1 x 10/3

1 pool is filled in time = 10/3 hours

This means, if both John and Matt fill the pool together they will take 10/3 hours which is 3 hours and 20 minutes to fill the pool.

A shortcut to solve such questions is:

Time taken to fill the pool = (Product of individual times)/(Sum of individual times)

Time taken to fill the pool =
`(5(10))/(5+10)= (50)/(15)= (10)/(3)`

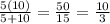
This results in the same answer as we achieved above.