Question

What is the area of this trapezoid? 96 in² 132 in² 168 in² 1344 in² Trapezoid A B C D with parallel sides D C and A B. Points F and E are between D and C. F E B A form a rectangle with 4 right angles. D F is 3 inches, F E is 8 inches., E C is 3 inches., E B is 12 inches., and A B is 8 inches.

Answer 1

Option B. 132 inch²

Explanation:

Since we know the formula to calculate the area of trapezoid is =
`(1)/(2)(height)(base)`

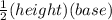
where height of the given trapezoid ABCD is side BE and two parallel sides are AB and DC.

It's given in the question

Side BE = 12 inches

AB = 8 inches

DC = (DF + FE + EC) = (3 + 8 + 3) = 14 inches

Now we put these values in the formula

Area of trapezoid ABCD =
`(1)/(2)(AB+CD).(BE) = (1)/(2)(8 + 14).(12)=(1)/(2)(22)(12)=(11).(12)=132`

Therefore answer is Option B. 132 inch²

Answer 2

Answer
132 〖in〗^2


Explanation
Although the diagram was not given, I was able to get it in the internet.
The area of a trapezium is found by the use of the following formula:
Area =1/2 h(a+b)
Where h is perpendicular distance between the two parallel lines, while a and b is are the lengths of the parallel lines.
In this question;
h=12 in
a=8 in
b=3+8+3=14 in
Area =1/2×12(8+14)
=6×22
132 〖in〗^2