Question

What is the sum of the arithmetic series 18 t=1 (3t-4)

a. 234
b. 441
c. 25.5
d. 49

Answer 1

The given arithmetic series is

`\sum_(t=1)^(18) (3t-4)`

When t =1, we will get the first term,a, which is

`3(1)-4 =3-4=-1`

When t =18, we will get the last term,l , which is

`3(18)-4 = 50`

Now we use the formula of sum of n terms which is

`S = (t)/(2) (a+l)`

Substituting the values of t,a and l, we will get

`S = (18)/(2) (-1+50) = 9*49 =441`

Answer 2

Consider the arithmetic series
`_(t=1)\Sigma^(t=18) (3t-4)`

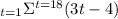
Let t=1 in the given series, we get

first term =
`a_(1)` = 3-4 = -1.

Let t=2 in the given series, we get

second term =
`a_(2)` =
`(3 * 2)-4 = 2`

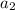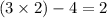
Let t=3 in the given series, we get

third term =
`a_(3) = (3 * 3)-4=5`

Now, let t=18 in the given series, we get

last term = l =
`l = (3 * 18)-4 = 50`

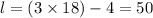
We get the series as

-1, 2, 5,..... 50

Sum =
`(n)/(2)(a+l)`

=
`(18)/(2)(-1+50)`

=
`= 9 * 49`

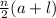
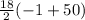
= 441

Therefore, the sum of the given arithmetic series is 441.