Question

The volume of a cones is 6 pie, if a cylinder has the same diameter and height as the cone what is it's volume?

Answer 1

`\bf \begin{array}{llll} \textit{volume of a cone}\\\\ V=\cfrac{\pi r^2 h}{3} \end{array}\qquad \qquad\qquad \begin{array}{llll} \textit{volume of a cylinder}\\\\ V=\pi r^2 h\implies 3\left((\pi r^2 h)/(3) \right) \end{array}`

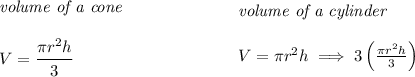
now, notice, the volume of the cylinder is really about the same as the volume of a cone, just 3 times larger, assuming "h"eight and "r"adius for both is the same amount.

now, if we know the cone with that "h" and "r" has a volume of 6π, the cylinder is.... well, you already know.