Answer:
The answer is (2,1)
Explanation:
Given a vector in the plane, we can describe the rotation as a function :
X is the vector
T is the function that represents the rotation
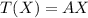
Where A is the rotation matrix
The rotation matrix about the origin in counterclockwise sense for an angle ''a'' is :
![A=\left[\begin{array}{cc}cos(a)&-sin(a)\\sin(a)&cos(a)\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/ol4tx0pkrqqk401dabo6a0ozdwqvn50bfa.png)
If we replace ''a'' by 90 ⇒
![\left[\begin{array}{cc}cos(90)&-sin(90)\\sin(90)&cos(90)\\\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/cnzfdzhih6zpd7v1k41lzzmbbykryzhltz.png)
![A=\left[\begin{array}{cc}0&-1\\1&0\\\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/6ry179jhyfclqvgdnf4asma89bpk3pnc9p.png)
If we want to rotate the vector D = (1,-2) :
![T(D)=AD=\left[\begin{array}{cc}0&-1\\1&0\\\end{array}\right]\left[\begin{array}{c}1&-2\end{array}\right]=\left[\begin{array}{c}2&1\end{array}\right]](https://img.qammunity.org/2019/formulas/mathematics/high-school/b1tbikevroc2dw1kpzq1wqtevob80hj1dc.png)
The rotation of the vector (1,-2) about the origin for an angle of 90 and in counterclockwise sense is (2,1)