Question

Which absolute value function has a graph that is wider than the parent function when graphed represents the parent function f(x)=|x| reflected over the x-axis and translated 1 unit to the right

A. F(x) = -|x|+1
B. F(x) = -|x-1|
C. F(x) =|-x|+1
D. F(x) =|-x-1|

Answer 1

The answer to this is B

Answer 2

B.
`F(x)=-\mid{x-1}\mid`

Explanation:

We are given that a function

`f(x)=\mid x\mid`

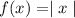
We have to find absolute value of function when parent function reflected over the x- axis and translated 1 unit to the right.

The transformation rule when the point (x,y) is reflected over x- axis is given by

`(x,y)\rightarrow (x,-y)`

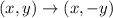
Apply the reflection on function over x- axis then, we get

`g(x)=-\mid x\mid`

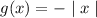
Transformation rule when the point (x,y) is shifted a units towards right is given by

`(x,y)\rightarrow (x-a,y)`

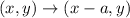
When the graph is translated 1 units towards right then , obtained function is given by

`F(x)=-\mid{x-1}\mid`