Answer: The correct answer is (B) 0.5.
Step-by-step explanation: Given that A(5, 3) , B(3, 7) and C(1, 4) are the vertices of ΔABC and A′(2.5, 1.5) , B′(1.5, 3.5) and C′(0.5, 2) are the vertices of ΔA'B'C'.
We are to find the scale factor of the dilation of the centre of dilation is origin.
We know that the scale factor of dilation is given by the following formula:
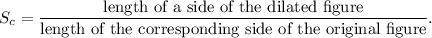
We can calculate the lengths of the corresponding sides AB and A'B' of ΔABC and ΔA'B'C' respectively using distance formula as follows:
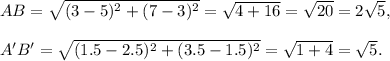
Therefore, the scale factor for the dilation is given by
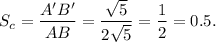
Thus, the required scale factor is (B) 0.5.