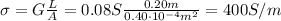Question

Find the conductivity of a conduit with a cross-sectional area of 0.40 cm2 and a length of 20.0 cm if its conductance G is 0.080 units.

Answer 1

4.0

Step-by-step explanation:

Answer 2

The equation that relates the conductance G with the conductivity
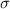
`\sigma` is given by

`G=\sigma (A)/(L)`
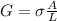
where A is the cross-sectional area while L is the length of the conduit.
In our problem, the area is
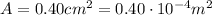
`A=0.40 cm^2=0.40 \cdot 10^(-4)m^2` and the length is
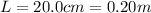
`L=20.0 cm=0.20 m`, while the conductance G is
`G = 0.08 S`, therefore re-arranging the equation we can find the conductivity:

`\sigma = G (L)/(A)=0.08 S (0.20 m)/(0.40 \cdot 10^(-4)m^2)=400 S/m`