Question

PLS CHECK IF MY ANSWER IS CORRECT! 40 POINTS!

Question:
A circuit (picture attached) is shown. If Light Bulb A is removed, what would happen to the brightness of the other light bulbs (B, C, D)? Assume the resistance of each resistor to be R, and the total voltage to be V.

My answer:
The total resistance before A was removed:

`R_t = ((1)/( ((1)/(R))+ ((1)/(R)) + ((1)/(R )) ))+R = (4)/(3)R`
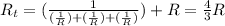
The total resistance after A was removed:

`R_t = ((1)/( ((1)/(R))+ ((1)/(R)) + ((1)/(R )) )) = (1)/(3)R`

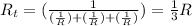
Total Current before A was removed:

`I = (V)/(R) = (V)/( (4)/(3) R) = (3V)/(4R)`
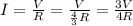
Total Current after A was removed:

`I = (V)/(R) = (V)/( (1)/(3) R) = (3V)/(R)`

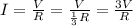
Current of Light Bulb B before A was removed (and C & D because they have same R and V as B):

`V = V - ( (3V)/(4R)*R) = V - ( (3V)/(4) ) = (1)/(4) V`

`I_B = (V)/(R) = (V)/(4R)`

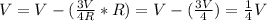
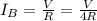
Current of Light Bulb B after A was removed (and C & D because they have same R and V as B):

`V = IR = V - (\frac{3V}R} *R) = V - 3V = -2V`

`I_B = (V)/(R) = (-2V)/(R)`

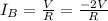
So, since
`(-2V)/(R) \ \textless \ (V)/(4R)`, the brightness of B, C, and D decreases because the current of all of them decrease.

Answer 1

As someone who is taking an electrical theory course in college, your total resistances and total currents are definitely correct. Furthermore, your final statement is correct (given that your lightbulb currents are correct).

I'm not completely sure if your current in the lightbulbs are correct because I'm pretty "Brain-ed" out from the semester and electrical theory isn't my best subject. I'd double check with some friends on those two statements.

I think the trouble is that I'm having a hard time following your logic. Overall, it appears you do have logical reasoning. Hope I helped a bit!