Question

There are 20 goldfish in a pond. Their population is increasing by 20% each year. The same pond has 100 minnows. The minnow population is increasing by 10 minnows each year. Make a graph to find the year that the two species of fish will have the same population. In what year will the fish populations be approximately the same?

Answer 1

The graph is attached, showing the intersection point at 13.5 years and populations of 235.2 for each population.

We only consider the portion of the graph from x=0 on, since negative time is illogical. Tracing the graph we get the intersection point.

Answer 2

13.5 years.

Explanation:

We know that exponential growth function is in form
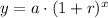`y=a\cdot(1+r)^x`, where, a is initial value and r is growth rate in decimal form.

Population of goldfish after x years would be
`y=20\cdot(1+0.20)^x`.

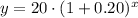We know that a linear function is in form
`y=mx+b`, where, b is initial value and m is slope.

Population of minnow after x years would be
`y=100+10x`.

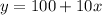Graphing both equations, we will get our required graph as shown in the attachment.

Since both graphs intersect at
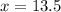`x=13.5`, therefore, in the 13.5 years both populations will approximate the same.