Question

Place the indicated product in the proper location on the grid.

(3a + 2c )(9a 2 - 6ac + 4c 2 )

Answer 1

The product of
`\left(3a+2c\right)\left(9a^2-6ac+4c^2\right)=8c^3+27a^3`

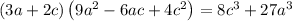
Explanation:

Given: Polynomial
`\left(3a+2c\right)\left(9a^2-6ac+4c^2\right)`

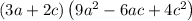
We have to place the indicated product in the proper location o the grid.

Consider the given product
`\left(3a+2c\right)\left(9a^2-6ac+4c^2\right)`

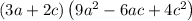
Using distributive property, Multiply each term of first bracket with each term of last bracket, we have,

`=3a\cdot \:9a^2+3a\left(-6ac\right)+3a\cdot \:4c^2+2c\cdot \:9a^2+2c\left(-6ac\right)+2c\cdot \:4c^2`

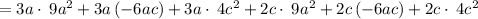
Apply plus-minus rule
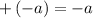`+\left(-a\right)=-a` , we have,

`=3\cdot \:9a^2a-3\cdot \:6aac+3\cdot \:4ac^2+2\cdot \:9a^2c-2\cdot \:6acc+2\cdot \:4c^2c`

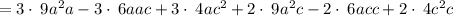
Simplify, we have,

`=27a^3-18a^2c+12ac^2+18a^2c-12ac^2+8c^3`

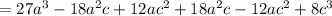
Adding similar terms, we have,

`=8c^3+27a^3`

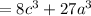
Thus, The product of
`\left(3a+2c\right)\left(9a^2-6ac+4c^2\right)=8c^3+27a^3`

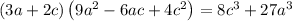
Location on grid is as shown below

Answer 2

Answer
27a^3+8c^3

Explanation.
In this question you are expected to expand (3a+2c)(9a^2-6ac+4c^2
(3a+2c)(9a^2-6ac+4c^2
=(3a×9a^2 )-(3a×6ac)+(3a×4c^2 )+(2c×9a^2 )-(2c×6ac)+(2c×4c^2 )
27a^3-18a^2 c+12ac^2+18a^2 c-12ac^2+8c^3
27a^3+8c^3
The expansion of the expression, (3a+2c)(9a^2-6ac+4c^2) is 27a^3+8. This is what the question requires.