Question

Keller boat travels 24mph. find the rate of the river if she can travel 6 mi upstream. in the same amount of time she can go 10 mi downstream.

Answer 1

Given that Kellen can travel upstream in the same amount of time she travels downstream, the rate of river will be found as follow:
time=(distance)/(speed)
time taken to travel upstream is:
(24+x)/10
Time taken to travel downstream is:
(24-x)/6
given that the time taken to travel upstream and downstream is the same then:
(24+x)/10=(24-x)/6
6(24+x)=10(24-x)
144+6x=240-10x
6x+10x=240-144
16x=96
x=96/16
x=6 mph

Answer 2

The correct answer is:

6 mph.

Step-by-step explanation:

We will use the formula d = rt for this, where d is distance, r is rate, and t is time.

We know that the time for both distances is the same; this means we want to isolate t in our formula. To do this, we will cancel r by dividing both sides:
d/r = rt/r
d/r = t

We will write an expression for the time upstream, an expression for the time downstream, and set them equal.

For the time upstream, the distance is 6 and the rate is 24-x; this gives us


`(6)/(24-x)`

For the time downstream, the distance is 10 and the rate is 24+x; this gives us


`(10)/(24+x)`

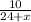
Together, these give us the equation


`(6)/(24-x)=(10)/(24+x)`

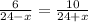
We cross-multiply to solve this:
6(24+x) = 10(24-x)

Using the distributive property, we have
6*24 + 6*x = 10*24 - 10*x
144+6x = 240-10x

Adding 10x to each side,
144+6x+10x = 240-10x+10x
144+16x = 240

Subtract 144 from each side:
144+16x-144 = 240-144
16x = 96

Divide both sides by 16:
16x/16 = 96/16
x = 6