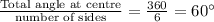Answer:
Measure of angle is 60°
Explanation:
Given when constructing a regular hexagon inscribed in a circle, we have to measure an angle formed by any two adjacent vertices of the hexagon and the center of the circle.
we have to find the measure of central angle of hexagon
Total measure of angle at centre is 360°
As polygon is given regular hexagon therefore central angle divides into six equal angles.
Hence, measure of an angle formed by any two adjacent vertices of the hexagon and the center of the circle is