Question

What is the length of CC' ?

Answer 1

The distance of CC' is 5.39 units.

Answer 2

The length of CC' is,
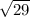`√(29)`units

Explanation:

Using distance(D) formula for any two points is given by:

`D = √((x_2-x_1)^2+(y_2-y_1)^2)`

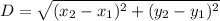
As per the statement:

From the graph:

The coordinates of C and C' are:

C = (2, 2) and C' = (7, 4)

Apply the distance formula to find length CC', we have;

`CC'= √((7-2)^2+(4-2)^2)`

⇒
`CC'= √((5)^2+(2)^2)`

⇒
`CC'= √(25+4)`

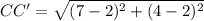
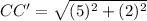
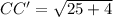
Simplify:

`CC'= √(29)`

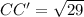
therefore, the length of CC' is,
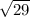`√(29)` units